Develop Parametric Architecture with Grasshopper

Grasshopper is an add-on or plugin for Rhinoceros 3D, created by McNeel, the developer of Rhino. It has been in test for a while, but is freely available. It uses .NET libraries from Microsoft, so it is not compatible with the ongoing OS X port of Rhino (yet). Current releases of Grasshopper are only available for Rhino 5.0 on Windows.

With Grasshopper, the “history” features of Rhino are used. Initially, the geometry you create in Rhino is not dynamic, in the sense that as soon as a surface or curve is generated from other geometry, this origin is lost. Since r4.0, you can turn on the history of Object creation, but it is difficult to control and visualize. The plugin “Explicit History” was meant as a GUI for this feature and it evolved into a full programming environment inside Rhino. The name changed to Grasshopper (each McNeel product has the name of an animal).

It is getting a lot of attention in architecture schools, in advanced practices and with designers and artists, worldwide.

Information & Websites

McNeel Website

Rhinoceros Website

Grasshopper Website + Gallery/Example

You will need McNeel Rhinoceros 5.0 Windows. The current release of Grasshopper is not available for older releases of Rhinoceros. You can download Grashopper for free, after providing an e-mail address.

Drag the downloaded RHI file onto the Rhinoceros interface to start the installer. Then you need to restart Rhinoceros to complete the installation. Type “grasshopper” on the command prompt and the first time, you need to accept the EULA.

If the floating window of Grasshopper is opened, the installation has succeeded.

Some questions about the Grasshopper software

There are different ways to do anything in Grasshopper (GH), but we can start simply with making a few points and use them to control curves (lines, splines).

Start with dragging a “Point XYZ” component onto the Canvas.

It is found on the “Vector” tab underneath the “Point” sub-pane. From now on, we will indicate this as “Vector > Point > Point XYZ”, but remember that these components are not found in the menu.

From here on, you can add a few sliders onto the Canvas which you can connect to the Pt Component we just placed. You drag from the “output” of the Slider onto one of the “inputs” of the Point XYZ Component. From there on you can interactively drag the slider to control the three coordinates of the Point.

You have a lot of control over the slider as well. By right-clicking the slider, you can access its settings:

• Name > ensure that you give a meaningful name now, before you forget what the slider is intending to do.

You have to imagine each slider as a “Parameter of your design”. This is the input you will manipulate to control the outcome. Give them meaningful names (e.g. “floor-height”, “amount of windows”).

• Accuracy > real, integer, even or odd + amount of digits
• Numeric Domain > min, max, range and value. Drag the counter up or down or double-click to type the value

Close the dialog again and the slider is fully set. While you drag the slider, you see the point displayed as a red cross in the Rhino viewports. You can not select it there, as it is only temporary geometry, controlled by Grasshopper. But you can zoom, pan and orbit to look at it.

Once you have made some geometry that you want to use further, you can always “bake” it from the GH interface.

Make a second point and connect both points using a Curve > Primitive > Line component.

While this is a complete parametric geometric design, it is also quite cumbersome when you need so many boxes for a simple line. But be patient. It will become better over time.

Something that may surprise you initially is the way different “boxes” are combined and what the effect will be.

The following example uses a single “Point XYZ” component and three number input boxes (“Params > Primitive > Number“). For each number box you can right-click and “Set Multiple Number” or “Manage Number Collection”. Define the first number box to contain the values 1,2,3 and 4 and the second to contain values 1,2 and 3.

When you combine two lists with different lengths, you have to tell Grasshopper how to combine both lists. If you don’t do anything, the default behaviour is to repeat the last element in the shortest list as many times as needed to ensure all additional elements in the longest list receive a value.

If you want to alter this behaviour, additional components are available to control this.

Remark: Most Grasshopper tutorials might still point to setting the combination behaviour on the level of the component receiving these lists, but this is outdated in the current release!

• When choosing the “Shortest List“, items from both input lists are combined, until one of the lists reaches the end.
• For the “Longest List“, values from the lists are combined in different ways, depending on the configuration of this component:
  • “Repeat Last” and “Repeat first” ensure the first or last item of the shortest list is repeated till the end of the longest list.
  • “Wrap” will repeat the items in the shortest list as many times as needed.
  • “Flip” will wrap the items forward and then backward again, as many times as needed.
• A “Cross-Reference” list makes all possible combinations of both lists using different algorithms: “holistic”, “diagonal”, “coincident” etc

While you can ‘manually’ insert individual numbers and points, it is more productive to make lists and series of items in most cases.

Imagine you would like to create a large amount of individual lines. It would be cumbersome and non-productive to define all their inputs one-by-one. That would be more efficient to draft or model.

Imagine following piece of code, which could be Java or C++ or many other languages. This is precisely the kind of control a textual programming language offers and that we want to apply also in Visual Programming.

if (int i = 0; i < 10; i ++) {...}

How would you do this in Grasshopper?

Let’s create a list of circles, each with a different radius using the “Sets > Sequence > Series” component.

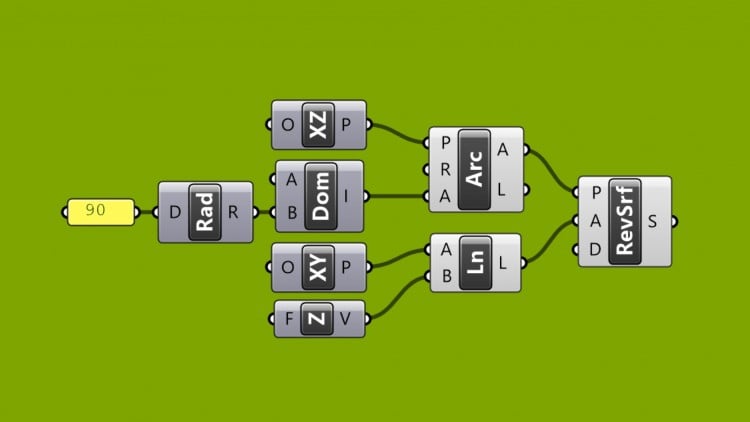
In another example, we generate multiple lines between two extreme points, using the “Sets > Sequence > Range” component, together with the “Math > Domain > Domain” component, which can be used to define lower and upper bounds of a numeric interval.

For simple sequential lists of numbers, the series and range components are quite versatile. However, when you need to create more mathematically complex curves, you can write a Formula.

“Math > Script > F1(x)” is a formula with one variable (x). There are F2(x,y) and F3(x,y,z) components too. And even one with n-variables, if you want to use it.

The following example evaluates a F1(x) function “Sin(x)” for a Range of Points XYZ, defined by the Domain [-10,10] in 34 steps. The points are connected through an Interpolated Curve.

Tip: With Formulas, it is advisable to copy the formula text into a Panel and link that to the Function Component. This makes your Grasshopper project more legible, as you don’t have to open the Component to see which function is being used inside.

Now would be a good time to start playing with some other functions, e.g. in more variables.

When you have a series of entities, they are accessible as a list. There are several operations you can perform on lists: pick one item from the list, reverse the list, shift all the values, pick a sub-list, merge lists…

The following small example draws a few circles (using a range and domain, point and circle).

The slider lets you control which of the circles will be chosen, using “Sets > List > List Item“.

The resulted curve will then be extruded to a cylinder, using a “Vector > Vector > Unit Z“, magnified with a fixed number (the extrusion height).

More complex control over which items to pick from a list, can be found in the Split, Cull and Cull Pattern components. E.g. you can define that you want one every third item from a list to be passed through.

Moving, rotating and scaling objects is done with Transformations.

Remark: One important thing to consider when using Transformation is that Grasshopper creates new items when you transform one. E.g. when you have a curve that you transform, you will arrive with both the original curve and the transformed one. You can always disable the “Preview” option of the object you don’t want to see in the result (while still requiring it for the calculations).

The next example draws a single box and makes a series of transformed copies, which could act as the floor in a simple tower.

While you can do a lot with series, ranges and functions, sometimes you want a more intuitive control, something more visual. We are architects, after all and prefer visual thinking.

“Params > Special > Graph Mapper” is a component which allows you to control a series of values visually, as a function. Typical examples include linear, sine, parabola and even Bézier curves.

The next example displays a similar set as the transformed floors, but modifies the scaling of each successive box. We had to add a few more tricks too:

• ensure that the series of input points for the graph mapper is a linear range between 0 and 1
• set the Graph Mapper to type Bézier, to have manual control
• ensure the scaling centers are at the centers of the box (use the Z-vectors we already had)
• have the same amount of points in the graph > we subtracted 1 from the Stories variable

Remark: While it can be tempting to have some numbers hardcoded, try to ensure that the whole solution stays valid for the slider inputs you have defined. You have to set sensible min and max values and check that each variation of the sliders can be calculated. Be careful with list that might have different amount of values!

Some questions to see if you understood this section

Reference: This example is based on [A.Tedeschi (2011), Parametric Architecture with Grasshopper, Chapter 5.4]

While you can make a full parametric design using only Grasshopper, sometimes it is more convenient to work with Rhino geometry. You can pick surfaces, curves and points from Rhino and use them inside your Grasshopper solution. When you modify the geometry inside Rhino, the GH solution is updated.

Typical examples are using a few curves to generate a loft. When you define the curves in Rhino, you can still tweak them afterwards, with all the resulting geometry updating in (near) real-time, depending on the size of your project.

In this example, we will use a Loft surface and use a “Params > Geometry > Surface” component. Right click and choose “Set One Geometry”. GH is temporary hidden to allow you to pick an object in Rhino.

Since you now see both the Rhino and the GH surface, we can disable the Preview of the GH Surface component, to not clutter the viewport (right-click on the component to access this option).

This surface has to be re-parametrized first, for this procedure to work. This means that the internal UV coordinates will be remapped to the range (0..1), which is important for the following steps.

You can set this on the component itself, with the “Reparameterize” option. This is also indicated on the canvas by a small icon, resembling a Gaussian curve.

Since we want to split our Surface into smaller pieces, we need to sub-divide it.

The “Math > Domain > Divide Domain2” component can do that for us. While it looks as if it is meant for list of numbers, it works well on NURBS surfaces, which have an internal UV coordinate grid. Add two sliders to control the amount of steps.

We’ll use this subdivided surface to place “Transform > Morph > Surface Box“, which creates twisting boxes that follow the surface closely. You can add an additional height parameter to control the thickness of the shell we are creating.

This gives us a subdivide surface, with the contours of the twisted boxes, which we will use to morph something else into.

While the boxes on themselves are not that interesting, we will use them primarily as guiding geometry to twist and bend our Reference Geometry into. The “Morph” component will deform an input geometry, so its bounding box fits inside the target geometry. Since all the boxes over the surface are twisted, our reference geometry will be morphed into all the different deformed target boxes, but the corners will still fit with the neighbour boxes.

In the next example, we create a simple 4-sided pyramid in Rhino and reference this into a “Params > Geometry > Geometry” component. We can finally add the “Transform > Morph > Box Morph” component.

The Reference geometry is linked to its two first inputs S (Base Geometry) and D (Reference Geometry), whereas the Surface Boxes are linked to the last parameter T (Target Boxes).

This example could be further extended. When you want to use several objects grouped for the Reference geometry, you will have to insert a BoundingBox component before the R-parameter of the Morph component. Try to come up with some nice variations and see how far you can stretch or twist the results.

Remark: Beware that each individual morphed box has a different shape, which would be unfeasible in traditional, manual modeling. This is a typical example of the advantage of a parametric approach.

Another nice extension to this example is using not a single but multiple Reference geometries, to alternate the panels on the surface.

Before you can do this, you need to insert a “Sets > List > Long List” component, which you can set to different modes to steer how the short list (the reference geometries) and the longer list (the Surface Boxes) can be combined into combinations.

Here we set it to wrap, which ensures that the first surface box receives the first Reference Geometry, the second the second, the third the third and the fourth surface box receives the first Reference Geometry again (and so forth).

Now the re-generating of the final geometry can really take several seconds to generate. So instead of sliding the value of the slider, double-click it and enter it by typing (so not all in-between values are being calculated).

This example is based on [A.Tedeschi (2011), Parametric Architecture with Grasshopper, Chapter 6]

This exercise is a (slightly revised) variation on the example cited above. It is a remake of a design by Santiago Calatrava, for a high-rise twisted skyscraper. The tower itself is actually built and is the largest residential tower in Sweden.

We will focus on getting this fairly complex project organized, starting from a simple outline, into a twisted volume. Some of the details are skipped, as to mainly discuss how to tackle this exercise as a designer.

We start with two basic curves inside Rhino, but (with some imagination) they could have any shape and could be fully created and managed inside GH as well. Ensure you have two closed (!) curves. You can draw them as single segments and use the join command in Rhino to ensure they really are closed with no gaps.

The first step is loading the outer curve from Rhino into GH and “move” it, using a series of Z-vectors, to make multiple copies. We introduce some variables (floor-to-floor distance, floor-count) and group these components in GH to visually modularize our script.

The Series links the “heights” to a Z-Vector component, which ensures the Move operation to receive multiple copies. Beware that the initial curve is visible in Rhino, is also visible inside the Crv-component (which you could hide) and is also part of the Move component, as the first height-value of the series is “0.0”.

This first series is “nested” into a new series of vertical copies. We have to hide the first one, to avoid overlapping geometry and also ensure we use a "Cross Reference" component to have all floors properly copied into all sectors.

We introduce some new variables with sliders and remember to give them meaningful names. The first “Move” component is hidden.

But this is not a correct solution. We need to ensure that all floors from the “Sector 1” group are displaced vertically and we introduce a “Cross Reference” component in between the two move components.

And there is a second problem: with this approach, we can have overlaps between the floors, e.g. when there are too many floors or the sector-distance is too low. Let’s add an additional calculation, so we calculate the total height of the first group of floors and use the “sector-distance” as the distance between two groups of floors. To do that, we get the final item from the Series list and add the sector-distance to it.

The central core of the tower is a simple vertical extrusion (“Surface > Freeform > Extrude“), using a Z-vector as direction and the total height as extrusion length.

You could make it a bit more clever, by making the “core-height” parameter only the extension above the final floor and use some math to add the total height between all floors.

Now we will introduce an overall rotation angle (here set at 180°). Before we can rotate the floor outlines, we have to calculate the individual rotation of each one of them, using a series and a division calculation. Re-use the floor- and sector-count sliders to calculate the total amount of rotations we need, as to find the rotation of a single floor.

Remark: For legibility, we can modify wire display into “faint” or even “hidden” (as in a wireless connection).

“Transform > Euclidian > Rotate Axis” is used to do the actual rotation. The Axis is created as a line, starting in the main “Vector > Plane > XY-plane” and using a Z-vector to indicate the second point. Only the position and direction is important here, not the length.

Remark: Don’t forget to translate the angle into Radians for the rotation! (“Math > Trig > Radians“).

This is really straightforward: extrude the series of outlines.

We simplify things a bit, by not subtracting the “core”. This is ideally done in advance.

For the facade, the Loft surface is a good candidate. However, we have to re-organize our series of curves quite a bit to loft only the curves per sector and not for the whole tower at once.

Remark: Here we also diverge quite a bit from the book, to do it all in a single step. The book repeatedly splits the list and lofts these extracted lists. We try to have a more flexible and adaptable solution.

Let’s hide everything we don’t need right now and focus on the series of outlines, which we want to loft, in clusters/sectors. It helps if you try to find a generic way of deciding how to split the list of floor into groups or sub-lists that belong together.

We try to come up with a single list, split per sector, with the sequence of floor outlines grouped. While we already have the full list of floor outlines, we want them grouped per sector. So we use a SubSet (“Sets > List > Sub List“) component, which requires the original list (the rotated floors) and a Domain to define the sub-list.

The creation of the Domain is the real clever part, here. It is not a single Domain, but defined from a series. The Series is created, starting from zero and will increase “floor-count” times with each step. This is repeated “sector-count” times. The result is a list containing the indices of each first floor of each sector (0, 6, 12, 18 in our example). You could easily write this out manually, but then it has to be adapted if you play with the floor- and sector-counts (which is what we want to do when exploring our solution space).

These numbers define the lower indices of the different domains we are creating. The higher numbers are then created from the floor-count, but “minus 1″ (a fixed yellow panel as input to make it legible). This number is added to each of the starting indices of the sectors, giving us the final floor index for each sector (e.g. 5, 11, 17, 23).

The domains are thus (0..5, 6..11, 12..17, 18..23).

The Final result, although not fully legible in the screenshot, shows the connections and how we tried to keep everything still fairly organised. Grouping components and giving them labels and different colours helps.

Remark: use labels, meaningful names, grouping and basic layout to clarify your script as much as possible. If you can’t decipher it yourself, then no-one can.

The biggest problem are the very long links from parameters far into the network. You could connect them to number containers at several steps, to avoid too much overlapping lines. But modularisation is one of the most important goals you have to reach. Even if the whole solution is only used in a single design, you have to be able to adjust and re-structure when entering changes. It is good to know that many designers are not really well-trained programmers and that these networks tend to become so complex that people start all over again, rather then trying to turn an existing script into an adapted one. However, if there are groups of components that you often use, they might be good candidates for pre-programmed components.

The "Remote Control Panel" is a nice feature to add some chosen sliders directly in a Rhino Panel, so you can minimise Grasshopper while exploring the solution.

We also show how to add some color to the generated geometry, using a "Custom Preview" component.

You can play with the parameters, but beware that this solution is getting closely out of real-time territory… When experimenting, use lower numbers for floor- and sector-count and maybe disable some components you don’t need (e.g. central core and floor extrusions).

Until now, you used mostly geometric components, numbers and some sliders. With series and ranges, you could control multiple objects. However, sometimes you need to dive deeper into the data mangling routines. In Grasshopper, data inside the components is fairly well structured. Apart from a component which caries a single value, most inputs/outputs can carry lists of values. In their simplest form, they are just like arrays, containing a row of numbers. However, sometimes the values are actually stored in lists that are stored in other lists. Like multi-dimensional arrays.

The visual metaphor of how the data is laid out is quite well explained by the Grasshopper creator David Rutten in the Tree diagram he made to explain how data inside Grasshopper is organised.

Data is stored as the leafs on a branch. Branches can be nested inside other branches. Each individual value (item) can be located and described using a path of numbers.

To assist you in seeing how your data is behaving, you can use the “Params > Special > Param Viewer” component and attach it to any output. Click on the Param Viewer and you get a nice, circular visualisation of the tree and its branches.

You can also attach a Post-It note/Panel to any output and see the tabular representation of the tree.

Whenever you have list of values (e.g. a series of curves or a series of numbers) you may want to inspect it first, before you start to use it and manipulate it.

Since you often have to manipulate these lists, a whole section of Components is available on “Sets > Tree“.

When connecting points with a curve, GH will only connect points that lie in the same “branch” of “path” of the data tree. There is no way to go from one path to another. In some cases, operations give you a branched tree.

The “Sets > Tree > Flatten Tree” removes all branches and places all values in a single branch. The Flatten option can also be set on an input of a component, to flatten the input from lists into a single list.

“Sets > Tree > Merge” (and its variations Merge 03 and Merge Multiple) allow you to combine streams from different components into a single list. Beware that merged lists will still contain different branches for each input, so you might have to combine this with a Flatten component in some cases.

“Sets > Tree > Graft” will turn an unstructured list (e.g. all values in a single branch) into a tree with multiple branches (e.g. each value in a single branch).

When you generate a series of curves and try to define a connection between them, you might struggle initially to get the right points connected.

The first example loads two Circles from Rhino into a “Curves” Component and subdivides them.

However, the result is not what you intended. You wanted to connect the corresponding point from the first circle with the corresponding point from the second circle.

You can use the “Sets > Tree > Path Mapper” component to define a translation that shifts elements between the branches of the tree.

In this case, the path of the first of the two points we want to connect was originally {0;0} and its index (0). The second point is {0;1}(0). We want them to be joined in a single path, as {0,0}(0) and {0;0}(1).

In the Path Mapper, you can type a generic path with placeholders and write in the target how it should be transformed.

Source: {0;a}(i) → Target: {0;i}(a)

Use a “post-it” component to visualise the results, to better see what you end up with.

There are much more complex things you can do and for this (common) basic example there is a preset component “Sets > Tree > Flip Matrix“. But once you grasp the Path Mapper, you can tackle most complex problems. Not with ease, though, but with perseverance.

This example can be perfectly extended for more curves. Try to add a third (and fourth) circle by your own and see how the same solution is reusable.

And finally, we will do something with the vertices we get. In this example, we simply create two lines between diagonal points and connect them to a “Surface > Freeform > Pipe” to give them a tube-shape. But you can do a lot more here, e.g. make a series of objects that react differently, based on orientation or length or whatever you choose.

While this does not solve all possible diagrids, this is a fairly simple and straightforward approach, upon which you can extend.

A complete different approach, using a series of rotated circles, can be found in following scheme. This is not applicable to apply on “any” freeform surface, though.

But it has some distinguishing features:

• the “pipes” run all the way through to the top and are thus continuous;
• this is completely made inside GH, so not need for Rhino Geometry (= full control);
• there is a visual control over the profile of the artefact, using a Graph Mapper component with Bézier handles.

Sometimes you need to connect different variables to a single parameter. Here we learn how to use the "Remap Domain" component, to turn one slider into two independent ranges, which control two separate parameters in another component.

This is a numerical example, which tries to find a suitable value for two sliders to get to the desired outcome. The absolute value of the difference of two sliders is calculated and Galapagos will try to minimise it. This will only succeed when both values become equal. This example has no use “as such”, but it explains how to set up and run Galapagos.

You connect the “Params > Special > Galapagos” solver as follows:

• the bottom link will ask a single numerical result. This is the target that Galapagos will try to either maximise or minimise.
• the left link has to be dragged to the “input” sliders, which can be tweaked by Galapagos to influence the target value.

Double-click the Galapagos Editor from the Component to set up the calculation.

• On the Options tab-page, you set the overall fitness goal (choose between “Minimise” and “Maximise”).
• On the Solvers tab-page, you can choose between available solvers and start the calculation.
• Finally, you can use the Record tab-page to inspect some of the results.

The editor is quite extensive and has to be seen in action to appreciate the visualisations.

You can re-instate any found solution, so you don’t have to agree on the numerical optimum as a designer, if you don’t want to.

This second example is a bit more practical. It creates a small tower, with a rounded rectangular floor plan. It is set up with all parameters properly constrained (e.g. Width of the tower can only vary between 10 and 20). The rounded is fixed, but the width, length and amount of floor levels can be varied by the solver.

The fitness function here is the absolute difference between the total floor area and a fixed level that is used to approximate.

The example contains a few tips as well:

• The rectangle is steered by two sliders, which both define a domain using a small expression: lower limit is “-A/2″ and the upper limit is “B/2″. This way a single slider can control the two values defining the domain.
• The total area of the floor is calculated using the “Surface > Analysis > Area” component (which also works for closed planar curves). All these areas are then summed using the “Math > Operators > Mass Addition” component. This is fed into a “Math > Operators > Absolute” component.

The next tips can help you in setting up a usable fitness function.

• If you have target values you need to reach (e.g. a required area), calculate their difference with the actual value, so “zero” would be the optimum. Using an absolute value allows you to minimise to that point. This allows you to adjust the target, without having to adjust the set value inside the solver.
• An alternative to set a desired outcome for a particular result is using a parabolic function (e.g. value * value). The minimum of this function would be the optimum. Negate it so the maximum would be the optimum.
• Yet another alternative is making a division. “1” would be the optimal result.
• When summing different criteria, the choice of weight values is quite important. Comparing pricing (in thousands of Euro) with area (in hundreds of square meters) with sizes (in tens of meters) would mean that pricing would always win the equation.
• Ensure that you don’t compare linear values with quadratic or cubic ones, as they evolve quite differently.